なぜ「対数平均温度差」なのか【化工のお部屋】

こんにちは。化工見習いです。

今回は、伝熱工学で出現する、「対数平均温度差」についてもう少し紹介したいと思います。

なぜ「対数平均」温度差なのか

対数平均温度差が出現するのは、以下の記事でも導出しましたが、これはただの数字遊びです。もう少し、本質的に捉えるべく、補足したいと思います。

あわせて読みたい

対数平均温度差の導出【化工のお部屋】 こんにちは。化工見習いです！ 今回は、対数平均温度差の導出を紹介していきます！！(スマホでは見切れるのでPC推奨) 対数平均温度差とは 対数平均温度差については、簡...

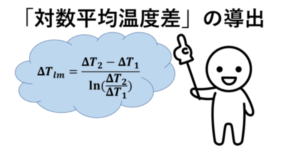
「なぜ、対数平均なんですか？」「なぜ、算術平均ではダメですか？」「なぜ、幾何平均ではダメですか？」と質問された場合、これは明確な回答があります。

「温度差の関数\(\ T_h(x)-T_c(x)\)が\(\ a^x\)の形であるから。」です。

温度差の合計は温度差の\(\ x\)方向積分で求められますが、これをフラットにして平均化するための手法が対数平均法です。

\(\displaystyle T_h(x)-T_c(x)=g(x)\)とすると、

\(\displaystyle \overline{g}=\frac{\int_a^{b} g(x)dx}{b-a}\)

これが、対数平均法の基本です。こちらのルートを押さえれば、ややっこい対数平均温度差の導出をしなくても解けます。

ちなみに、対数平均温度差を利用しなければ必ずしも平均化できないわけではありません。

所詮は\(\ a^x\)を平均しているだけですので、細かく区分して各温度差を算出し、それらを算術平均しても近い値を出すことが可能です。当然区分が細かければ細かいほど、算術平均温度差の結果は対数平均温度差に近づきます。

余談ですが、反応熱が存在する場合は、基礎式に基づけば、対数平均温度差が成立しなくなることが分かりますので注意です。

まとめ

熱交換における、温度差の平均化はなぜ、「対数平均」なのか

それは「温度差が\(\ a^x\)の関数だから」というか、それが対数平均法そのものだから。です

最後まで読んでいただき、ありがとうございました。