こんにちは。化工見習いです!
今回は、ガス吸収における重要な考え方である、二重境膜説と総括物質移動係数のついて簡単に説明しようと思います!
二重境膜説とは
二重境膜説とは、その名の通り「気相と液相に境膜が存在する」と仮定したモデルのことです。実際のガス吸収の機構はかなり複雑なので、簡単なモデルを仮定して、ガス移動速度を説明するわけです。
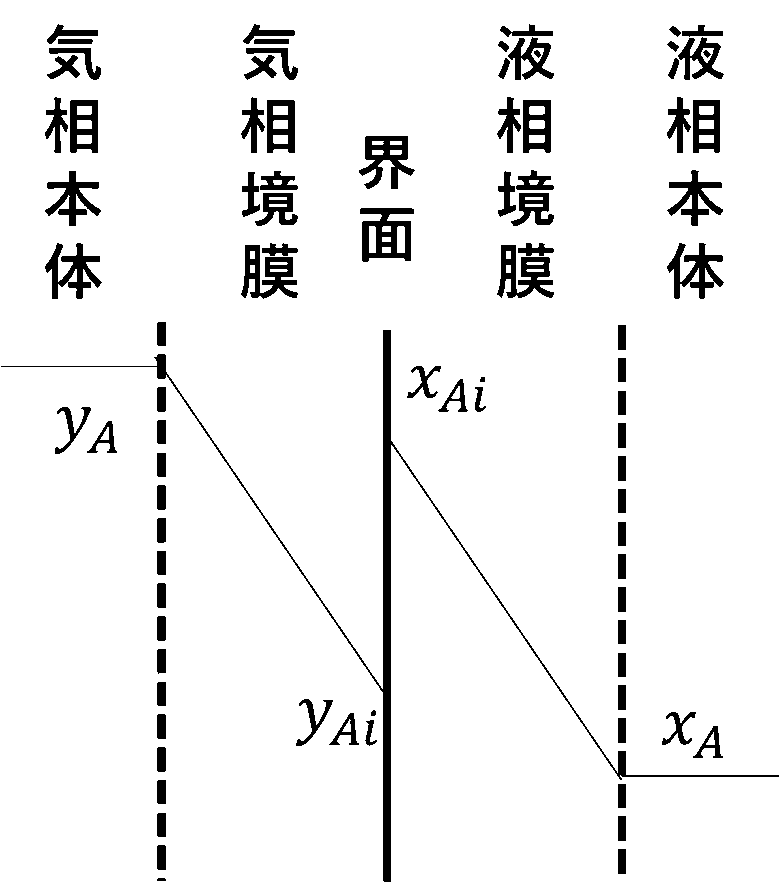
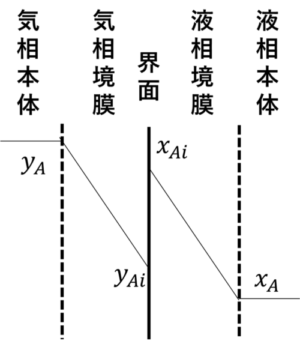
上図のように、濃度勾配が存在するのは両境膜の間のみで、そこには抵抗が存在すると考えます。
次に、界面とバルクでのモル分率差\(\ Δx\)を駆動力として物質移動は推進されるので、物質量流束は
\(\ N_A=k_x(x-x_i)=k_y(y_i-y)\)・・・(1)
\(\ k_x\):液相境膜の物質移動係数,\(\ k_y\):気相境膜の物質移動係数
\(\ x_i\):気液界面での液相モル分率,\(\ y_i\):気液界面での気相モル分率
と表されます。
しかし、この式から物質量流束を求めたくても、実際に気液界面の濃度\(\ y_i\),\(\ x_i\)を求めるのは難しいらしく、これでは困ったことになります。
総括物質移動係数
そこで、気液界面濃度を別の文字に置き換えてやる方法をとります。
ここで気液界面においてヘンリーの法則が成立しているとすれば
\(\ y_i=mx_i\)・・・(2)
\(\ m\):ヘンリー定数
が成り立ちます。また、気相と液相のバルクに対してもヘンリーの法則を用いると
\(\ y=mx^*\),\(\ y^*=mx\)・・・(3)
\(\ m\):ヘンリー定数,\(\ x^*\):\(\ y\)に対する平衡モル分率,\(\ y^*\):\(\ x\)に対する平衡モル分率
が成立し、気液界面濃度を(1)~(3)を用いることで消すことが出来ます。
計算は少し面倒ですが、それを終えると次の式が得られます。
\(\displaystyle N_A=\frac{mk_yk_x}{k_x+mk_y}(x^*-x)=\frac{k_xk_y}{k_x+mk_y}(y^*-y)\)
よって、以下のように置けば
\(\displaystyle K_x=\frac{mk_yk_x}{k_x+mk_y}\)
\(\displaystyle K_y=\frac{k_yk_x}{k_x+mk_y}\)
\(\displaystyle N_A=K_x(x^*-x)=K_y(y^*-y)\)
このときの\(\ K_x\)を液相基準の総括物質移動係数、\(\ K_y\)を気相基準の総括物質移動係数と呼びます。\(\ k_x\),\(\ k_y\)は推算式があり、\(\ m\)についても実験値が大体の物質について調べられていますので、これで物質量流束が求められるということになります!
ちなみに、逆数の形にすると
\(\displaystyle \frac{1}{K_x}=\frac{1}{mk_y}+\frac{1}{k_x}\)
\(\displaystyle \frac{1}{K_y}=\frac{1}{k_y}+\frac{m}{k_x}\)
というよく見た形になり、\(\displaystyle \frac{1}{K_x}\)および\(\displaystyle \frac{1}{K_y}\)は\(\ K_x\),\(\ K_y\)の逆数なので、物質移動の抵抗の大きさを表します。
また、先ほどの式から、\(\ K_x\),\(\ K_y\)には次の関係も成り立つことがわかります。
\(\ K_x=mK_y\)
どちらの相が律速か
\(\displaystyle \frac{1}{K_x}=\frac{1}{mk_y}+\frac{1}{k_x}\)
このときの\(\displaystyle \frac{1}{mk_y}\)は気相抵抗、\(\displaystyle \frac{1}{k_x}\)は液相抵抗を表していて、\(\displaystyle \frac{1}{K_x}\)は気相抵抗と液相抵抗の和を意味します。(\(\displaystyle \frac{1}{K_y}\)も同様。)
したがって、\(\ m\)が大きいときは\(\displaystyle \frac{1}{K_x}≓\frac{1}{k_x}\)となり、液相律速となり、逆に\(\ m\)が小さいときは\(\displaystyle \frac{1}{K_x}≓\frac{1}{mk_y}\)となり、気相律速となります。
まとめ
- 二重境膜説とは、液相と気相の両相に境膜が存在すると仮定するモデルである。
- 総括物質移動係数とは、片側を基準にしたときのガスの移動のしやすさを表したものである。
- 総括物質移動係数の逆数は、抵抗の大きさを表しており、気相抵抗と液相抵抗の和である。
今回は、二重境膜説と総括物質移動係数について簡単に紹介しました。
考え方自体は難しくないですが、式変形やヘンリーの法則など、基礎的な事が身についていないと追いつかないとは思うので、しっかり基礎から学ぶことが大切です。
最後まで読んで頂きありがとうございました!m(__)m