対数平均温度差の導出【化工のお部屋】

こんにちは。化工見習いです！

今回は、対数平均温度差の導出を紹介していきます！！(スマホでは見切れるのでPC推奨)

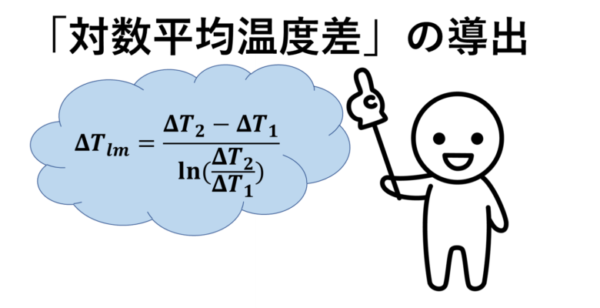
対数平均温度差とは

対数平均温度差については、簡単にこちらの記事にまとめてますので、ご覧ください！

あわせて読みたい

熱交換において、なぜ向流の方が効率が良いのかについて考察【化工のお部屋】 こんにちは、化工見習いです! 今回は算術平均温度差、対数平均温度差と向流並流の効率について少し書きたいと思います。 というのも、向流と並流の効率の違いについてず...

導出

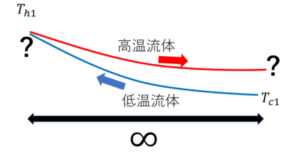
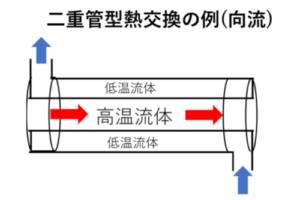
図のように、左（高温流入側）を1,右を2とする。

\(\ m\):流入流量, \(\ T\):温度, \(\ C\):比熱または熱容量, \(\ A\):伝熱面積, \(\ Q\):熱量

微小面積dAにおける、高温流体の失う熱量\(\ dQ>0\)、低温流体の得る熱量\(\ dQ>0\)を考えると、

\(\ dQ=h(T_h-T_c)dA=-m_hC_{p,h}dT_h=±m_cC_{p,c}dT_c\)

よって

\(\displaystyle dT_h=-\frac{dQ}{m_hC_{p,h}}\)

\(\displaystyle dT_c=±\frac{dQ}{m_cC_{p,c}}\)となり、

\(\displaystyle d(T_h-T_c)=-\frac{dQ}{m_hC_{p,h}±m_cC_{p,c}}=-\frac{hdA}{m_hC_{p,h}±m_cC_{p,c}}(T_h-T_c)\)

よって

\(\displaystyle \frac{d(T_h-T_c)}{T_h-T_c}=-\frac{hdA}{m_hC_{p,h}±m_cC_{p,c}}\)

\(\ T_h-T_c=ΔT\)として積分すると

\(\displaystyle ln(\frac{ΔT_2}{ΔT_1})=-\frac{hA}{m_hC_{p,h}±m_cC_{p,c}}\)

また、交換熱量\(\ Q>0\)は

\(\ Q=m_hC_{p,h}(T_{h1}-T_{h2})=±m_cC_{p,c}(T_{c2}-T_{c1})\)

よって

\(\displaystyle \frac{1}{m_hC_{p,h}±m_cC_{p,c}}=\frac{T_{h1}-T_{h2}+T_{c2}-T_{c1}}{Q}=\frac{ΔT_1-ΔT_2}{Q}\)

よって 

\(\displaystyle ln(\frac{ΔT_2}{ΔT_1})=-\frac{hA}{m_hC_{p,h}±m_cC_{p,c}}=\frac{hA}{Q}(ΔT_2-ΔT_1)\)

したがって

\(\displaystyle Q=hA\frac{ΔT_2-ΔT_1}{\displaystyle ln(\frac{ΔT_2}{ΔT_1})}=hAΔT_{lm}\)

対数平均温度差\(\ ΔT_{lm}\)は

\(\displaystyle ΔT_{lm}=\frac{ΔT_2-ΔT_1}{\displaystyle ln(\frac{ΔT_2}{ΔT_1})}\)

最後に

この導出が聞かれることはほぼ無いと思います。要するに「微小区間において①高温および低温流体の交換熱量は等しい(\(\ dQ=m_hC_{p,h}dT_h=m_cC_{p,c}dT_c\))ことと②その熱量は高温および低温流体の温度差に比例する(\(\ dQ=(T_h-T_c)hdA\))」ことを理解しておけば大丈夫です！

何か質問やコメントがあれば、宜しくお願い致します。