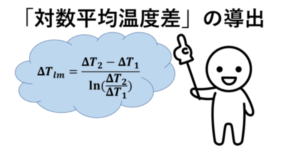こんにちは。化工見習いです!
今回は、熱交換器の長さをどんどん長くしていくと、最終的に流体の出口温度がどうなるのか気になったため、考えてみました。熱交換の記事は他にもあるので、良ければご覧ください!
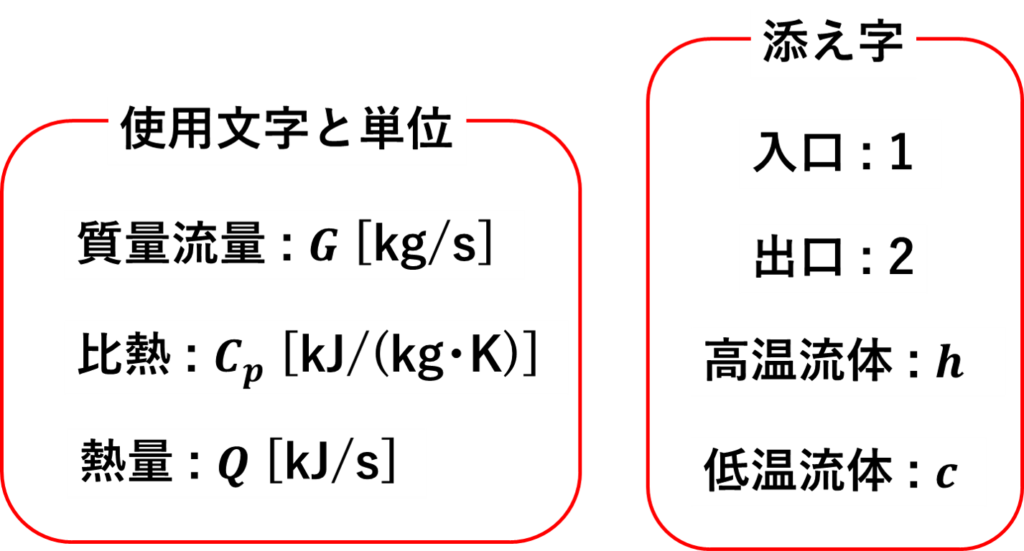
使用文字と単位、添え字の説明
まずは本記事における使用文字、単位、添え字の説明です。
考え方
まず大前提として熱交換における大事な3式があります👇
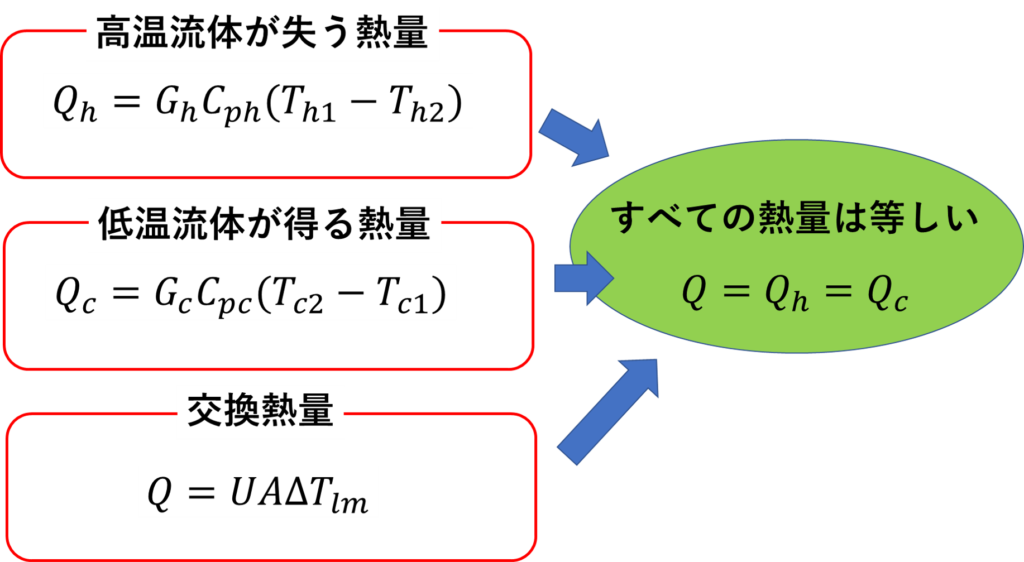
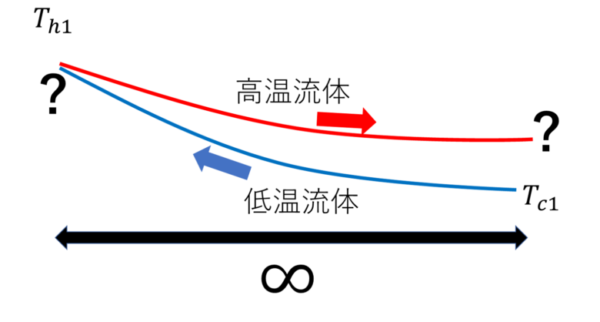
そして、熱交換器の長さを無限大に近づけると、対数平均温度差が無限小に近づくことが分かります👇

要は向流と並流それぞれにおいて、対数平均温度差が無限小に近づくような流体出口温度を求めてやれば良い、ということです。
対数平均温度差
では、対数平均温度差が0へ近づくような場合を考えてみます。


要は無限長における出口温度は、向流・並流にとってのΔTB=0で求められる、と言うことです。
並流
並流におけるΔTBは👇なので、
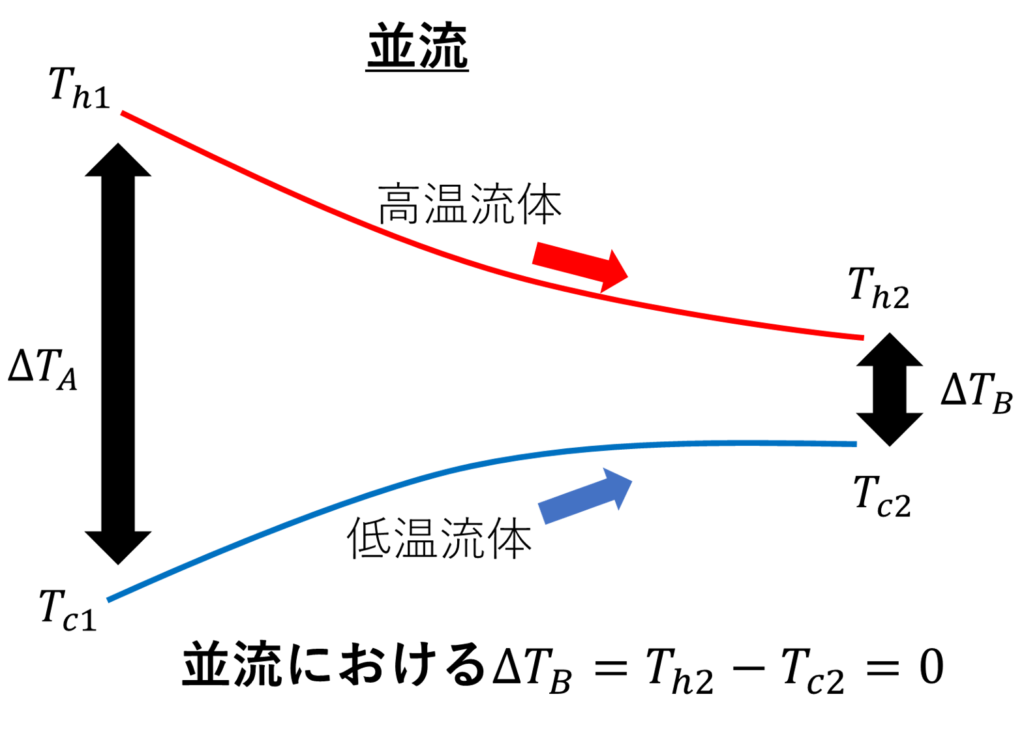
このように、並流では、両流体の出口温度が等しくなるように落ち着いていきます。あとはこれと最初に紹介した式から
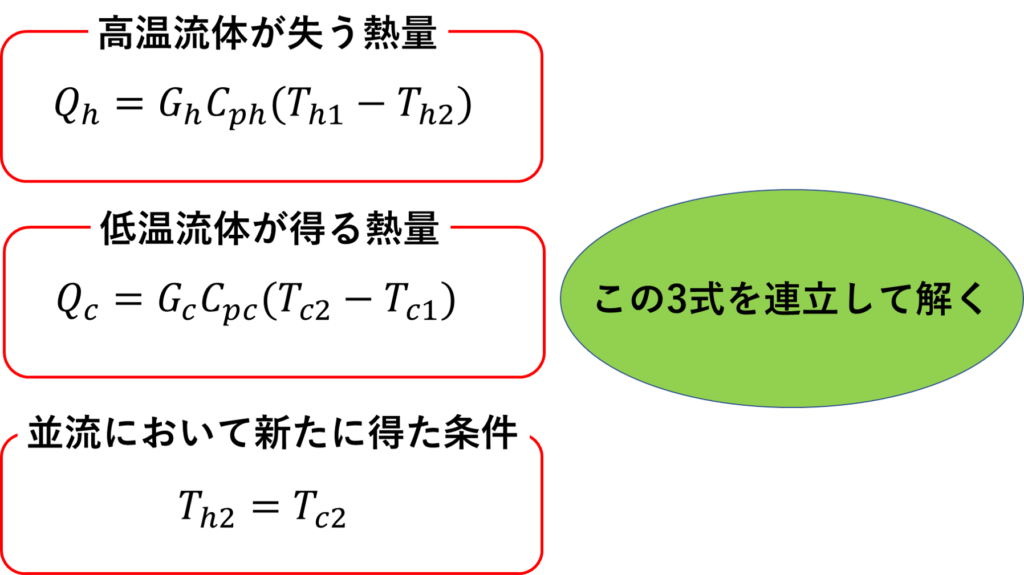

このように熱交換器無限長(並流式)での流体の出口温度を求めることが出来ました!
なんか重心みたいな式形になりましたね。
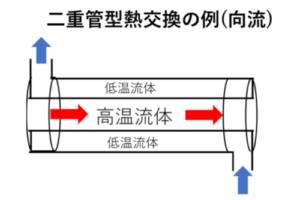
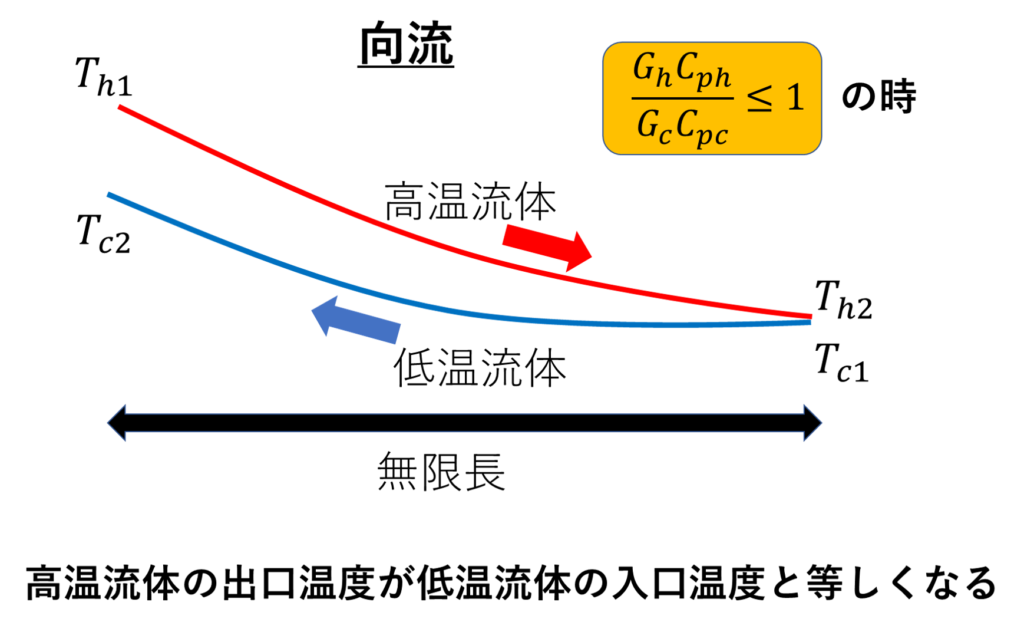
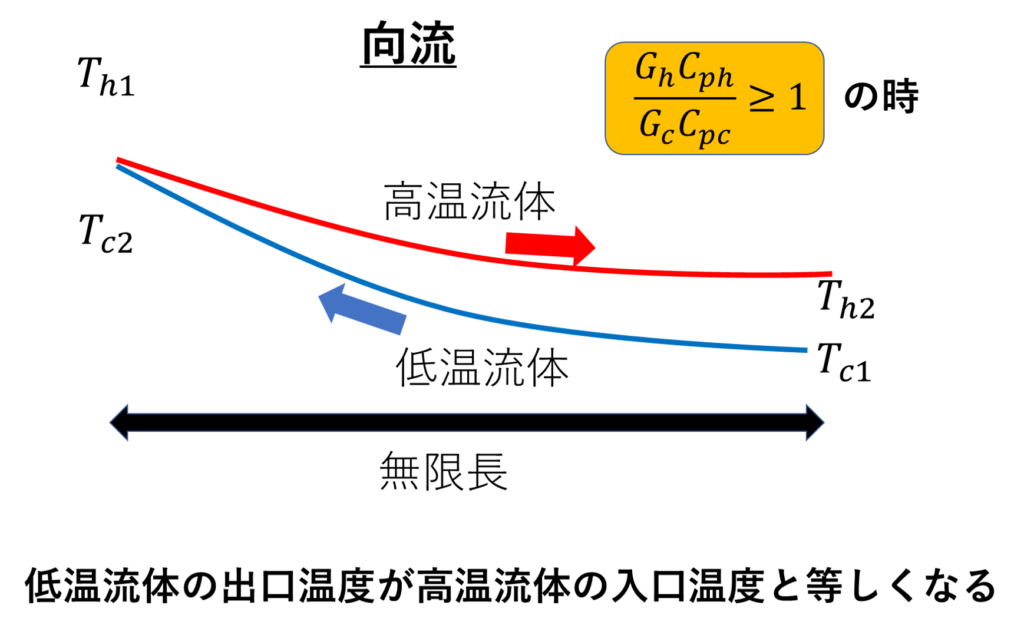
向流
対して、向流におけるΔTBは👇なので
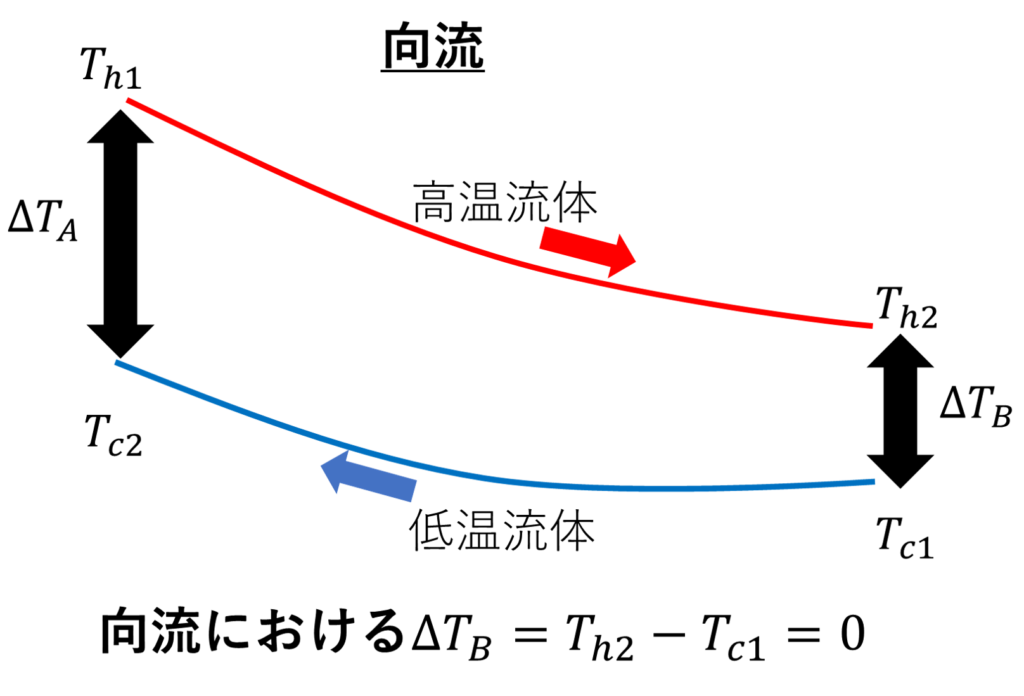
このように、高温流体の出口温度は低温流体の入口温度に近づきます。
㊟ただし、これは高温流体の熱容量<低温流体の熱容量の場合のみです!!(後ほど補足あり)
またまたこれと先ほどの式より
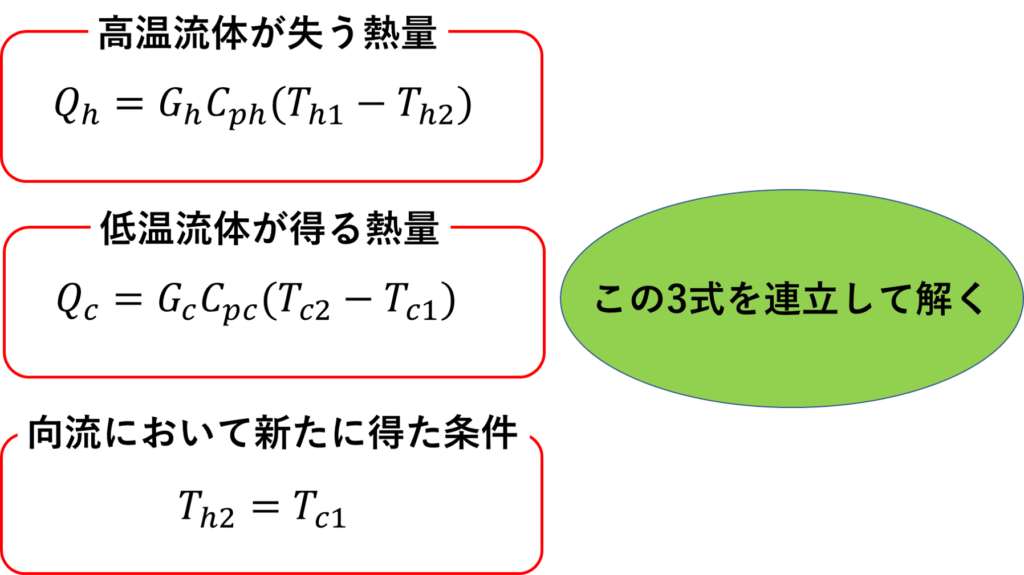

低温流体の出口温度が求めることが出来ます!
ここで先ほどの補足になります。今求めた解を分析してみます。
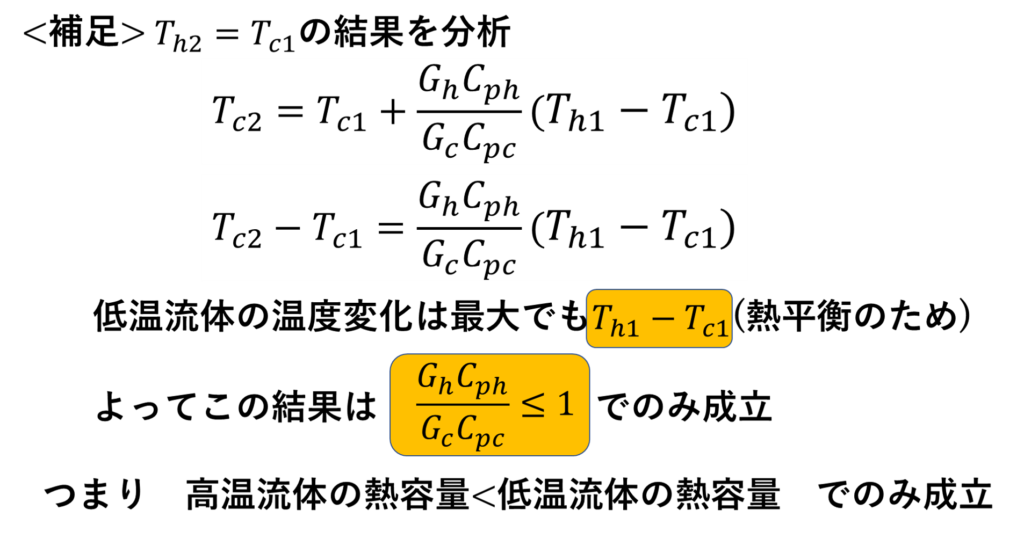
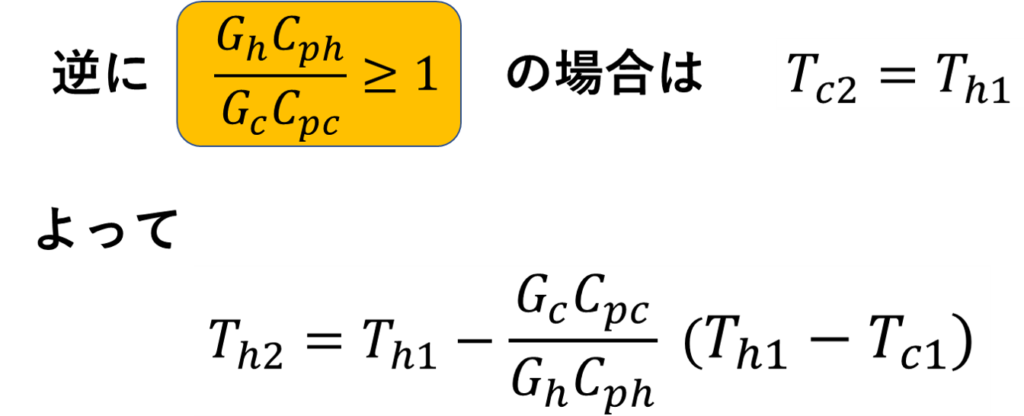
向流の場合はこのように、熱容量の大小関係で変わってくるようなので注意が必要です!
向流についてまとめるとこんな感じです👇
まとめ
並流では出口温度が互いに等しくなるところで落ち着く。
向流では、どちらかの流体がもう片方の流体の入口温度と等しくなるところで落ち着く。
ということが分かりました!今回も最後まで読んで頂き、ありがとうございました!!
熱効率が向流>並流である理由を数学的に考察しています👇