こんにちは。化工見習いです!
今回は、Newton域における重力終末沈降速度と遠心終末沈降速度を導出してみようと思います。
本記事の前半はStokes編、Allen編と同じものです。
Newton域
まずはNewton域の範囲を押さえます。粒子レイノルズ数\(\ Re_p\)の値によってStokes,Allen,Newton域に分けることが出来ます。
\(\ Re_p\leq2\)・・・Stokes域
\(\ 2<Re_p<500\)・・・Allen域
\(\ Re_p\geq500\)・・・Newton域
粒子レイノルズ数
Allen域の範囲が分かったところで、次に、粒子レイノルズ数の定義です。
\(\displaystyle Re_p=\frac{{\rho_f}\left|u-v\right|D_p}{{\mu}}\)
\(\ {\rho_f}\)は流体密度、\(\ u\)は流体速度、\(\ v\)は粒子速度を表します。
流体中の粒子の運動方程式
まずは前提として、以下の運動方程式が成り立ちます。
\(\displaystyle \frac{{\pi}}{6}D_p^3({\rho_p}-{\rho_f})\frac{dv}{dt}=-F_D+F_E\)
\(\ F_D\)は流体抵抗力、\(\ F_E\)は外力を表す。
\(\displaystyle F_D=\frac{1}{2}C_DA_p{\rho_f}(u-v)^2\)
\(\ A_p\)は粒子断面積であるので
\(\displaystyle A_p=\frac{{\pi}}{4}D_p^2\)
Newtonの重力終末沈降速度
Newton域では\(\displaystyle C_D=0.44\)。ここでは静止流体\(\ u=0\)を仮定します。
すると、\(\displaystyle F_D=\frac{1}{2}0.44\frac{{\pi}}{4}D_p^2{\rho_f}v^2=\frac{0.44}{8}{\pi}D_p^2{\rho_f}v^2\)
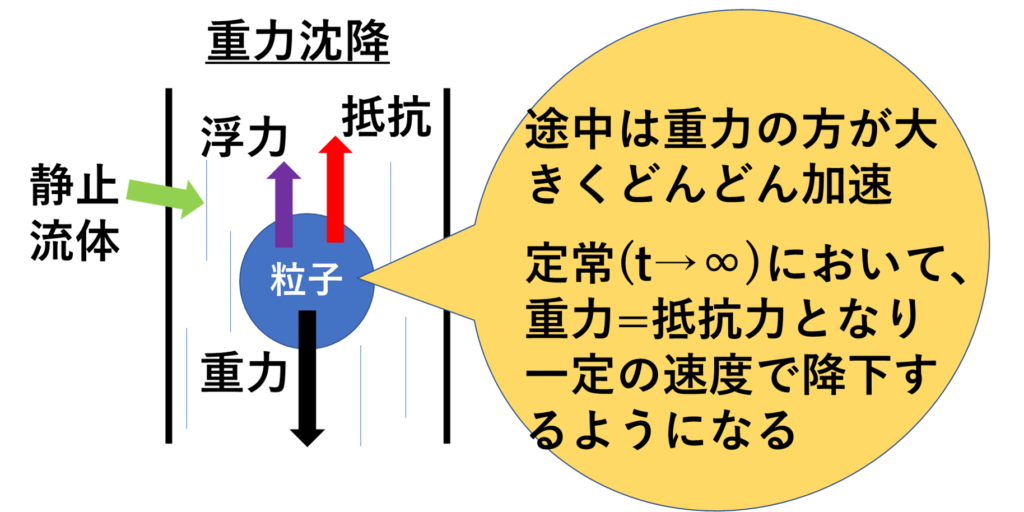
上のように重力場では外力は重力\(\displaystyle F_E=\frac{{\pi}}{6}({\rho_p}-{\rho_f})D_p^3g\)であるので
\(\displaystyle \frac{{\pi}}{6}({\rho_p}-{\rho_f})D_p^3\frac{dv}{dt}=-\frac{0.44}{8}{\pi}D_p^2{\rho_f}v^2+\frac{{\pi}}{6}({\rho_p}-{\rho_f})D_p^3g\)
この微分方程式を解くのは、Allenの時同様面倒なので終末沈降速度のみ求めます。
\(\ t→{\infty}\)で\(\displaystyle \frac{dv}{dt}=0\)より、重力終末沈降速度\(\ v_t\)は
\(\displaystyle v_t=[{\frac{3({\rho_p}-{\rho_f})D_pg}{{\rho_f}}}]^{1/2}\)
Newtonの遠心終末沈降速度
同様にNewton域で\(\displaystyle C_D=0.44\)。ここでも静止流体\(\ u=0\)を仮定します。
遠心力場では外力\(\displaystyle F_E=\frac{{\pi}}{6}({\rho_p}-{\rho_f})D_p^3r{\omega}^2\)であるので
\(\displaystyle \frac{{\pi}}{6}({\rho_p}-{\rho_f})D_p^3\frac{dv}{dt}=-\frac{5}{4}{\pi}{\sqrt{{\rho_f}{\mu}v^3D_p^3}}+\frac{{\pi}}{6}({\rho_p}-{\rho_f})D_p^3r{\omega}^2\)
\(\ t→{\infty}\)で\(\displaystyle \frac{dv}{dt}=0\)より、遠心終末沈降速度\(\ v_{tc}\)は
\(\displaystyle v_{tc}=[{\frac{3({\rho_p}-{\rho_f})r{\omega}^2D_p}{{\rho_p}}}]^{1/2}\)
終わりに
今回も最後まで読んで頂きありがとうございました!
何か質問などありましたらコメントの方よろしくお願いしますm(__)m
Stokes編はこちら👇

Allen編はこちら👇





