こんにちは。化工見習いです!
今回は熱伝導率kについて、その単位と意味について真剣に考えてみました。
「いや、そんなの分かるでしょ?」と思ったそこのあなた!本当にちゃんと説明できますか?
私が伝熱論を学んだ時に疑問をもったことで、一応自分なりの結論に至りましたので、今回記事にします。
Quiz
例えば下図のような状況を想定します。
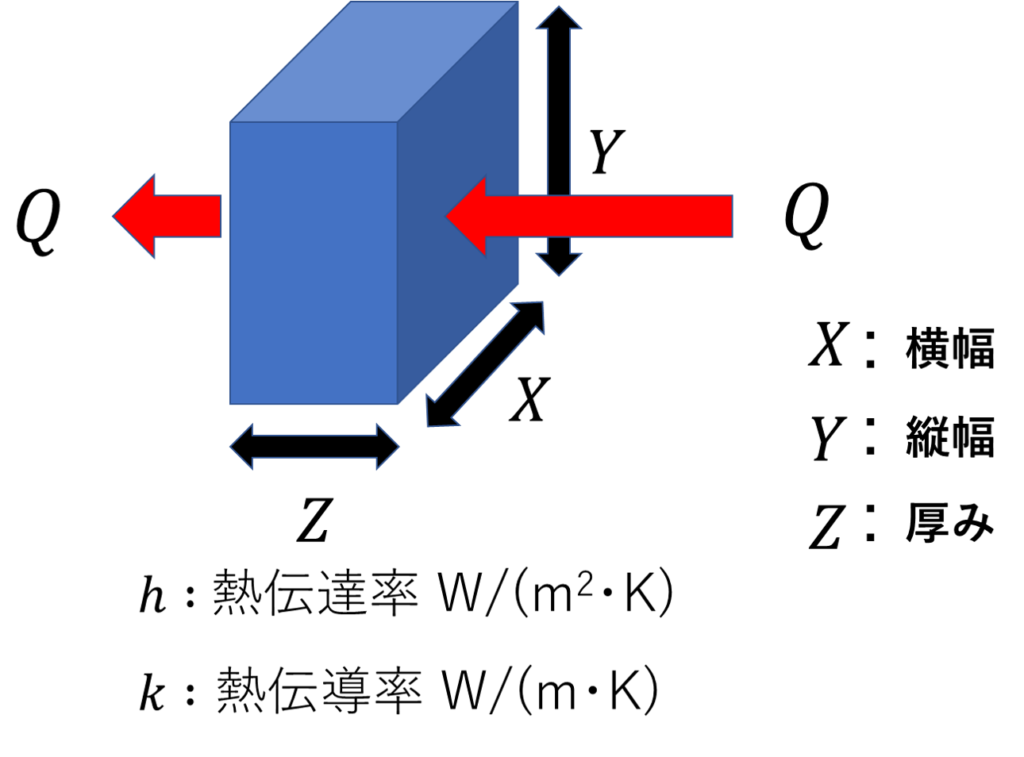
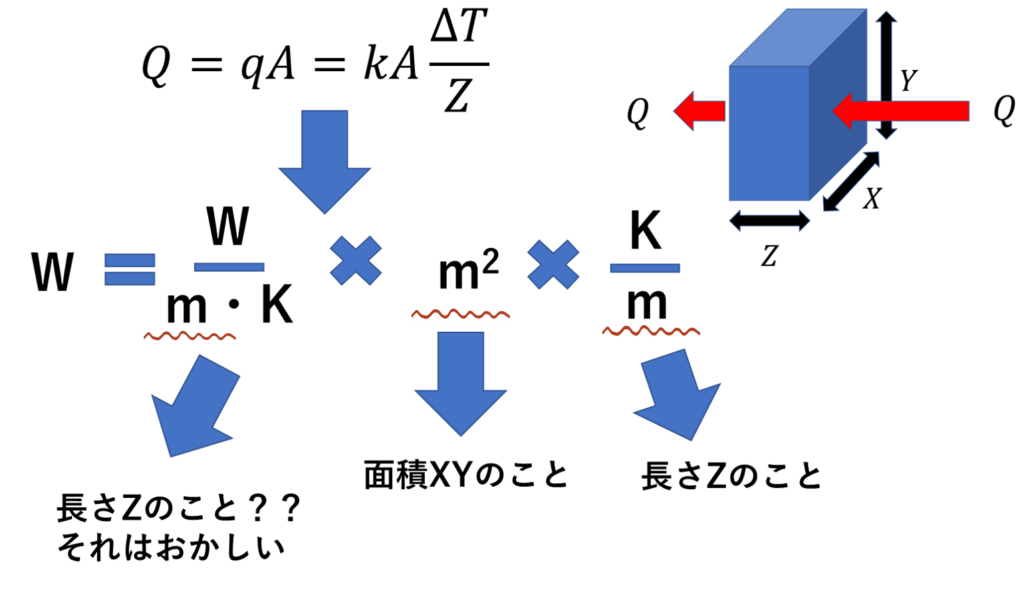
Qの方向に伝熱量が存在するとします。では、熱伝達率hの単位はW/(m^2・K)ですが、単位中のm^2とは、この図のどこを指すでしょうか?
もちろんXYで表される伝熱面積のことを指しますよね。
では、熱伝導率kはどうか。熱伝導率kの単位W/(m・K)のmとは、この図でいうと、どこの長さのことを指しているでしょうか?
正解は、、
Z(厚み)ではありませんよ。
私は伝熱論を学んだ当初、この図でいうところのZ(厚み)だと思っていました。kは厚み当たりの熱流量なんだと。そう思った方も意外とおられるのではないでしょうか?
でもよくよく考えるとそれはおかしいんですよね。
なぜ「厚み当たり」はおかしいのか
なぜ当時の私がおかしいことに気づいたかというと、
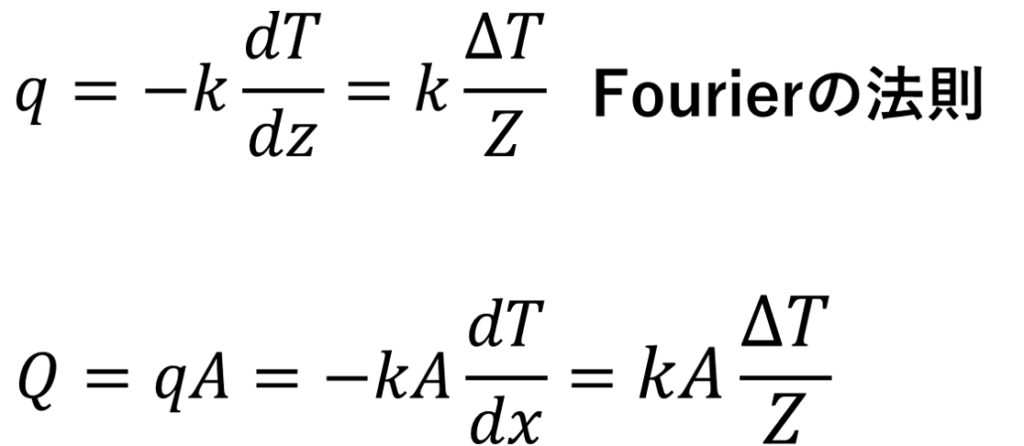
いわゆるこれはフーリエの法則といわれるやつですが、伝熱面積、温度差、それからkをかけて、それを長さ(ここは伝熱方向長さ)で割るという形になっています。Qについてここで次元を見てみると👇
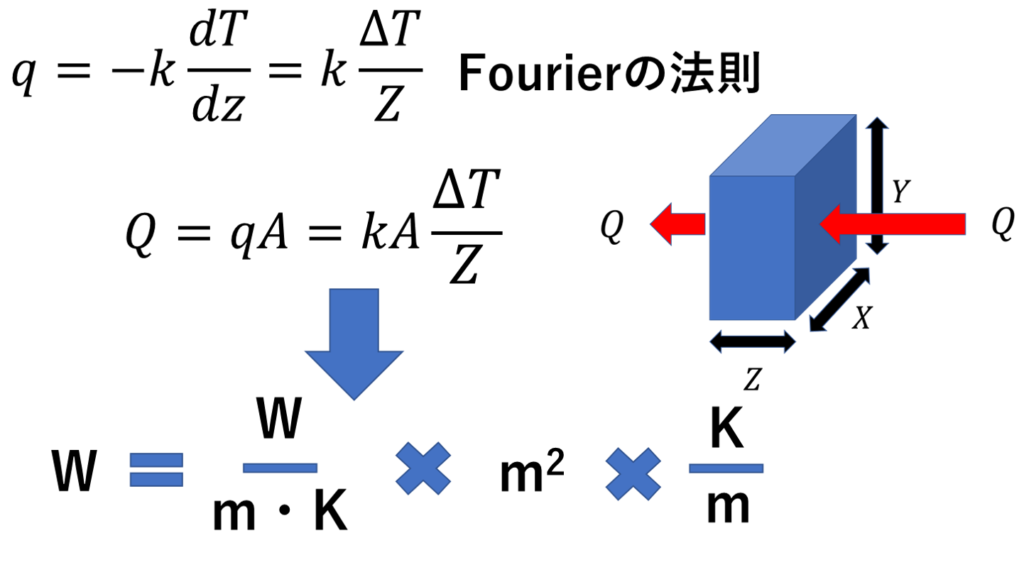
という関係が成り立っているわけです。ではさらに、長さの次元に注目してみると👇
このように、長さは長さでも、どこの長さを指しているかを整理すると、明らかに熱伝導率k中の長さは、Zではないことが分かります。
ではどう捉えるのが正解なのか
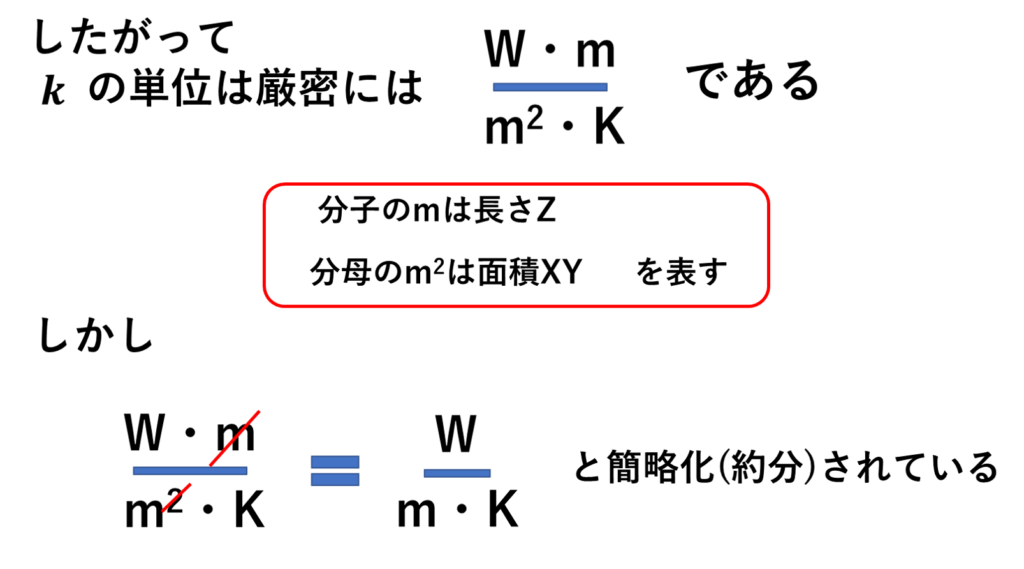
下図のように、W・m/(m^2・K)で、分子のmはZを、分母のm^2は伝熱面積XYを表すとすれば、つじつまが合います。ただ、「次元」だけ見れば確かに約分できるため、簡略化されてしまっていると思われます。👇
熱伝導率を日本語で的確に表現できるか
ではこれを踏まえて、熱伝導率を日本語でうまく表現できないか?と当初考えましたが、分からなすぎて諦めていました笑 今回ブログを始めて、ついに閃いた(別に普通のことですが)私の結論はこちらです。
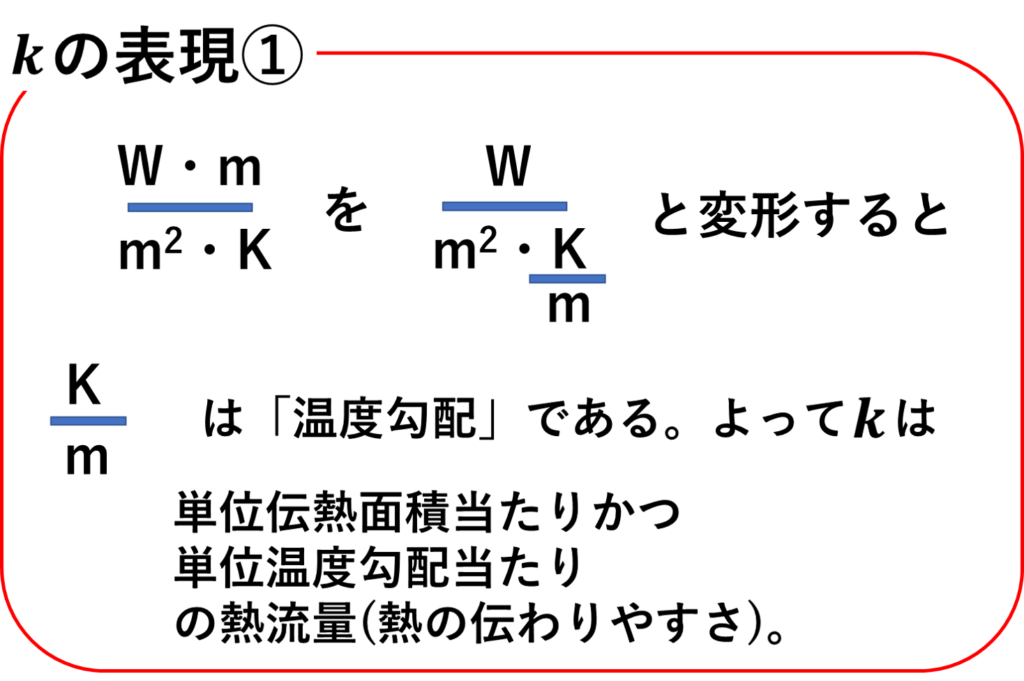
👆このように単位を変形することで、訳わからなかった分子のmがかなり扱いやすくなります。
よって熱伝導率kは「単位伝熱面積あたりかつ単位温度勾配あたりの熱流量」と表現することが出来ます。
さらにもう一つ、温度勾配が一定の場合は次のような言い方も出来るかと思います。
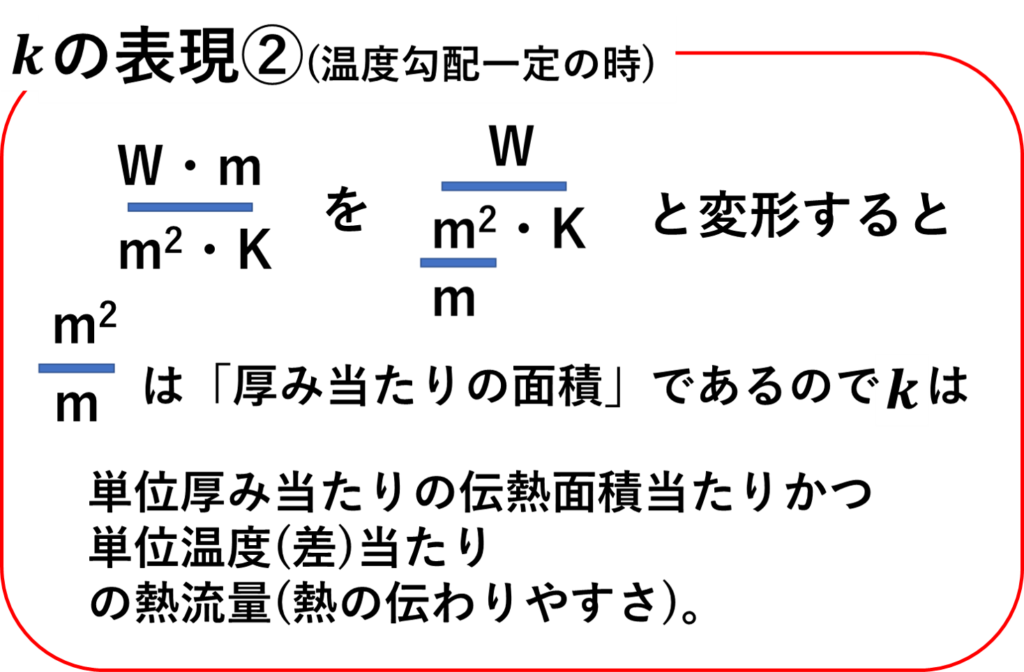
こちらの解釈であれば熱伝導率は、「「単位厚み当たりの伝熱面積」あたりかつ単位温度あたりの熱流量」ということになるでしょう。(多分) 一応「単位厚み当たりの伝熱面積」の補足を下に示します👇
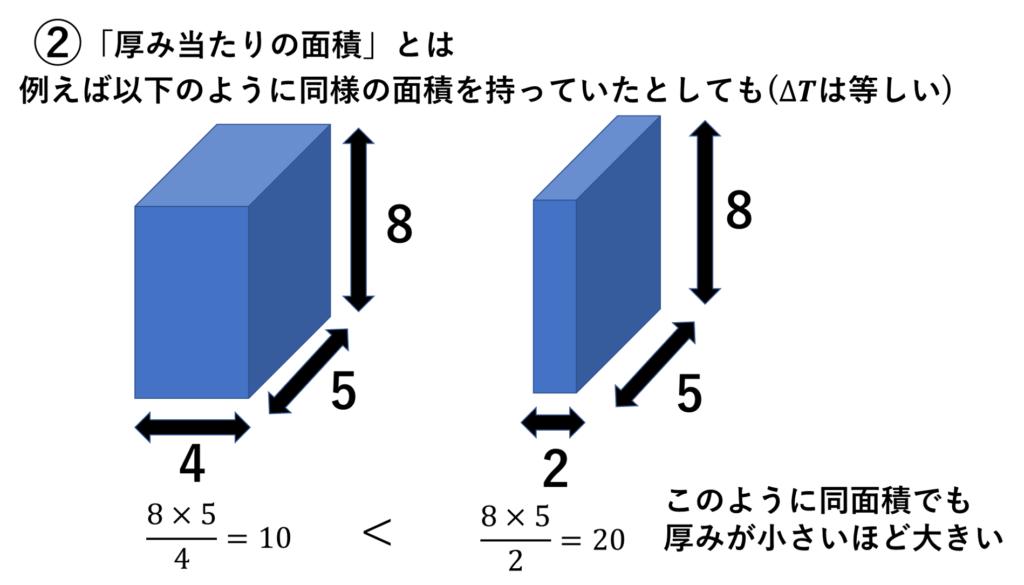
では、もう一度式を見返し、対流伝熱についての’当たり前’を伝導伝熱においても適用すれば

ちょーーーぜつ当たり前の事でした笑 情けない限りです><
ちなみに②は温度勾配一定としていますが、系全体では温度勾配が一定でない場合でも、一定と見なせるほど微少な区間まで刻めば、②の考えが適用できます。
それに熱伝導率は物質固有の値ですから、当然温度勾配も一定で(温度や材質によるkの変化は無視するとして)ややこしく捉えず、②の考えで良いと思います。
私と同じ勘違いをしていた方の参考になれば幸いです!
まとめ
熱伝導率kの単位中の分母のmは厚み(伝熱方向長さ)を表しているのではなく、厚み当たりの伝熱面積を表している。と言えるでしょう。
根本的なkとhの違い
最後に、kとhの根本的な違いですが、
熱伝導率kは固体(or液体or気体)の熱の伝わりやすさ
熱伝達率hは接する2種類の物質(固体-液体or固体-気体or液体-気体)間の熱の伝わりやすさ
です!
ということで、最後まで読んでいただき、ありがとうございました!!
他の記事も併せてごらんください!