レイノルズ(Re)数とは【化工のお部屋】

こんにちは。化工見習いです！

今回は、流動論でかなり始めに習う、レイノルズ数について簡単に説明したいと思います。

最初は円管内でのお話です。

レイノルズ(Re)数とは

レイノルズ(Re)数とは、以下で定義される「流れの乱れの大きさ」を表す無次元量となっています！

\(\displaystyle Re=\frac{{\rho}vD}{{\mu}}\)

そして、このレイノルズ数で求められる値が円管内の層流と乱流の状態をある程度教えてくれます。

\(\ Re<2300\)     層流

\(\ Re>3000\)     乱流

\(\ 2300<Re<3000\)     過渡状態(要するに層流と乱流の間)

＊この層流、乱流の境である2300や3000という数字(これを臨界値という)は、必ずしも一定ではなく、2300くらい,3000くらいという少し曖昧なものです。

したがって、教科書によってたまに違うことがあるので注意してください。

層流、乱流とはどのような状態か

念のため、層流と乱流がどのような状態を指すかについて紹介します。

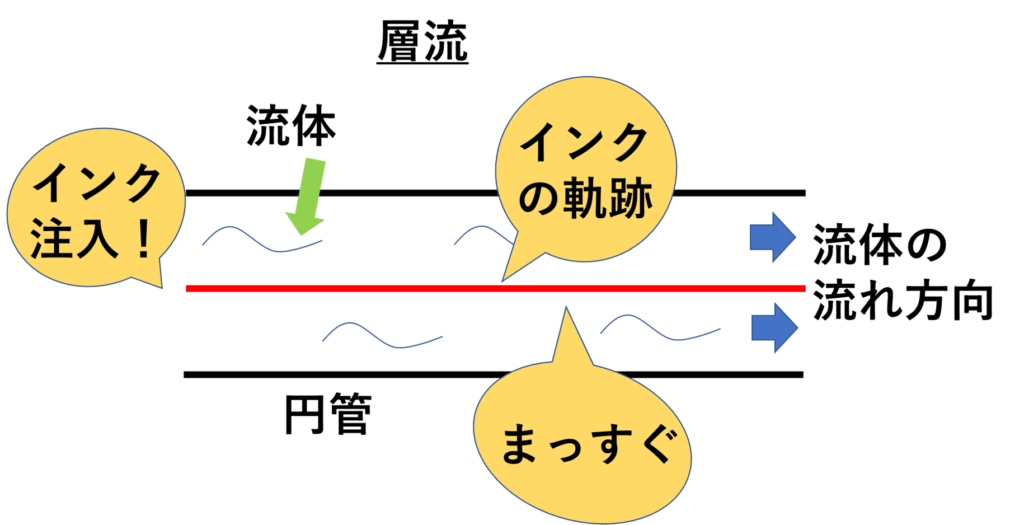
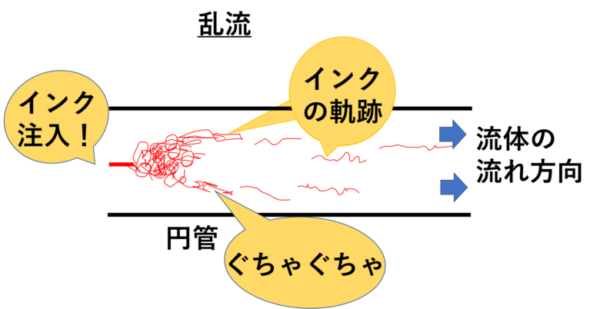
上のように、インクを円管の中心に注入して、そのインクの軌跡がまっすぐ1本になっている状態を層流といいます。対して

上の図のように円管内に注入したインクがバラバラに広がってしまう状態を乱流といいます。

＊絵が下手くそですみません笑

その他のレイノルズ数

円管の場合だけでなく、平板での流れやぬれ壁流れなどの場合についてもレイノルズ数が定義されています。

平板ではある程度先端から離れた距離\(\ x\)でのレイノルズ数が次式で定義されています。

　\(\displaystyle Re_x=\frac{xv_{\infty}{\rho}}{{\mu}}\)

\(\ Re_x<3.2×10^5\)・・・層流境界層

\(\ Re_x>3.2×10^5\)・・・乱流境界層

また、ぬれ壁流れなどの場合には次式で定義されます。

\(\displaystyle Re_x=\frac{4{\delta}\langle v_x \rangle{\rho}}{{\mu}}\)

\(\ \langle v_x \rangle\)は液膜の平均速度です。

\(\ Re<4～25\)・・・層流

\(\ Re<1000～2000\)・・・乱流

まとめ

レイノルズ数は「流れの乱れの大きさ」を表す無次元量である。

今回も最後まで読んで頂きありがとうございました！

本記事はこちらの「輸送現象」を基に作成しております。