こんにちは。化工見習いです!
今回の題材は、私がお世話になっている研究室に入る学生が必ずぶち当たる壁らしく、それについて考えてみましたので、まとめます。
Ω・m^2とは
事の発端は、自分がやっている実験で出てきた、[Ω・m^2]という単位。なんだこいつは?と先輩に聞いてみると、先生曰く「単位面積当たりの抵抗」だそう。
気になって調べてみると、「単位面積当たりの抵抗」だと言っている人もいれば、「S(面積)が分母に来ていないし、違うよ」と言っている人も。
先輩直伝の考え方と、自分の考えをまとめます。
先輩曰く
\(\displaystyle R=\frac{V}{I}\)
電流は面積によって変わる、\(\ I=i×S\)だから
\(\displaystyle i=\frac{I}{S}\)と変換してやって
\(\displaystyle R=\frac{V}{i×S}\)
\(\displaystyle RS=\frac{V}{i}\)
とここまで変換できれば、
\(\ i\):単位面積当たりの電流(電流密度)
\(\ V\):電圧(面積は影響しない)
ただの電圧を、単位面積当たりの物理量(電流密度のこと)で割っているのだから、その結果である\(\ RS\)は当然、「単位面積当たり」の抵抗だろう。
確かに言われてみればそうなんですけど。。
では、「単位面積当たりの」ってあるのに、なんで\(\displaystyle \frac{R}{S}\)ではなくて\(\ R×S\)なのか??
自分の考え①単位面積当たりとは-例①
そもそも単位面積当たりとは何かについて、例を挙げて考えてみることにした。
①物理量A(単位a)が、面積S(単位m^2)に比例するような現象があるとする。つまり\(\ A=B×S\)で表せる場合。(Bは比例定数)
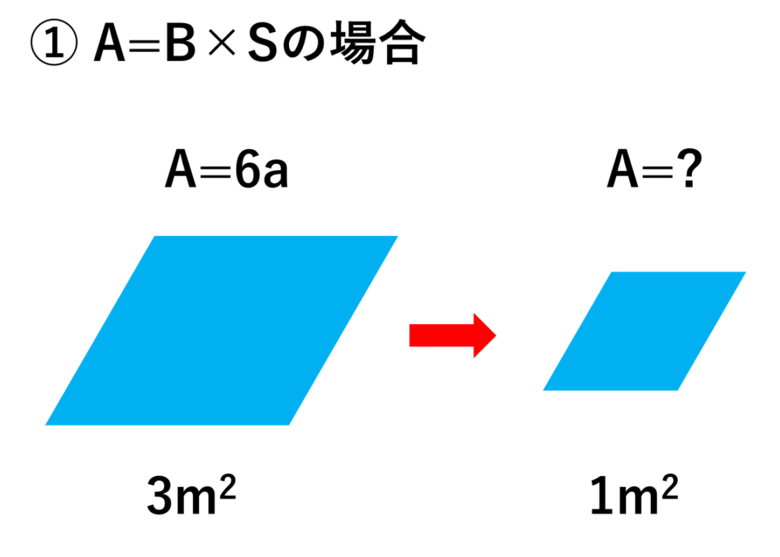
上図のように3m^2の時に、6aを示す時、単位面積当たりの物理量Aはいくらだろうかと考えてみると
単位面積当たりの\(\displaystyle A=\frac{6a}{3m^2}=2\) [a/m^2]
と当然のようにこう導く。
多分何も考えずとも物理量を面積で割り、\(\ 2\)[a/m^2]が計算できる。
しかし、その意味を考えてみると、
「Aは面積Sによって変わるから、面積を1m^2(単位面積)にそろえてね」ということで、本質的に、「1m^2用意したときAはどうなるのか」ということである。
これを踏まえて次の例を考えてみた。
例②
②では次に、物理量C(単位c)が面積S(単位m^2)に反比例する、つまり\(\displaystyle C=D×\frac{1}{S}\)で表せる場合を考えてみた。(Dは比例定数)
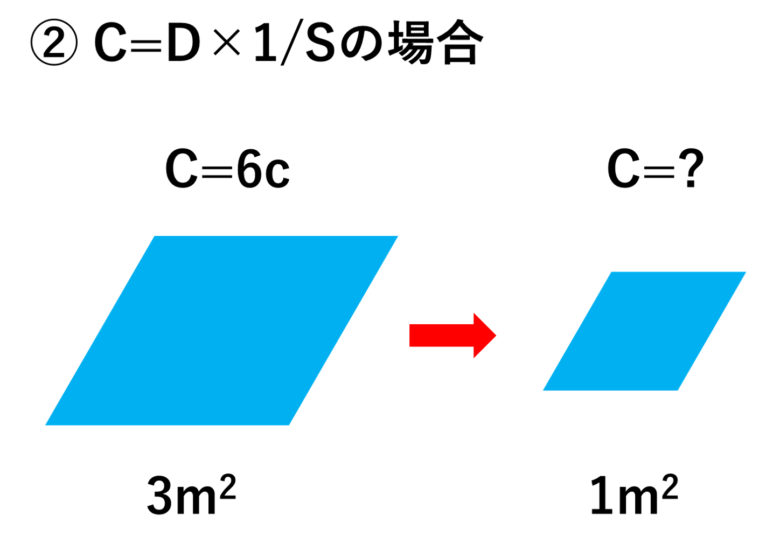
こちらも、3m^2で6cの時、単位面積当たりのCはいくらになるか。
こちらも、単位面積を用意してやれば、分かりやすい。
単位面積当たりの\(\displaystyle C=6c×3m^2=18\) [a・m^2]
となるはずであり、このようにCに面積Sをかける事となる。
つまりは、「単位面積当たり」が、「面積Sで割ること」なのか「面積Sをかけること」なのかは式により変わり、必ずしも「面積Sで割ること」ではない。
ということがこの例から分かる。
本題RS
では、本題の抵抗について
\(\displaystyle R=\frac{V}{I}\)
\(\displaystyle R=\frac{V}{i×S}\)
この形から、抵抗Rは面積に反比例する例②同じ形なので、面積当たりの抵抗は
\(\displaystyle RS=\frac{V}{i}\)
となる。
まとめ
単位面積とは1m^2(1cm^2や1mm^2もある)の事であり、
「単位面積当たり」とは「1m^2の時の物理量」を意味する。
RS(Ω・m^2)の物理的意味は「単位面積当たりの抵抗」である。