こんにちは。化工見習いです!
今回は、伝熱論で頻出の式などをまとめてみようと思います!
*本記事で紹介する式や事項は化学工学技士基礎に必要なレベルです。
フーリエ(Fourier)の法則
固体or液体or気体中での熱の移動の大きさは温度勾配に比例することを示した伝熱の基本的な式の1つです。
\(\displaystyle q=-k\frac{dT}{dy}\)
\(\ q\):熱流束[J/m^2・s],\(\ k\):熱伝導度[J/m・s・K],\(\ T\):温度[K]
ニュートンの冷却法則
固体-液体or固体-気体or液体-気体間での熱の移動を示した式です。
\(q=h\Delta T\)
\(\ h\):熱伝達率[J/m^2・s・K]
熱輻射
熱輻射による熱移動を示した式です。
\(q={\epsilon}{\sigma}T^4\)
\(\ {\epsilon}\):全輻射率[-],\(\ {\sigma}=5.67×10^{-8}\):ボルツマン定数[J/m^2・s・K^4]
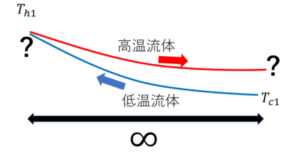
対数平均温度差
二重管型熱交換器などで温度差を平均化する式です。
\(\displaystyle {\Delta}T_{lm}=\frac{{\Delta}T_1-{\Delta}T_2}{\displaystyle ln\frac{{\Delta}T_1}{{\Delta}T_2}}\)
総括伝熱係数U
同面積の平板(長さLi)と境膜が連続している場合に、\(\ Q=UAΔT\)で表せるとすると
\(\displaystyle U=\frac{1}{\displaystyle \Sigma({\frac{1}{h_i}+\frac{L_i}{k_i}})}\)
内半径r1,外半径r2で熱伝導率kの円筒であれば、\(\ Q=U_1A_1ΔT\)で表せるとすると
\(\displaystyle U_1=\frac{1}{\displaystyle \frac{1}{h_1}+\frac{r_1ln(r_2/r_1)}{k}\frac{r_1}{r_2h_2}}\)
\(\ Q=U_2A_2ΔT\)で表せるとすると
\(\displaystyle U_2=\frac{1}{\displaystyle \frac{r_2}{r_1h_1}+\frac{r_2ln(r_2/r_1)}{k}\frac{1}{h_2}}\)
ヌッセルト(Nu)数
伝導伝熱と対流伝熱の比をとった無次元量です。
\(\displaystyle \begin{align} Nu=\frac{hD}{k}\\\\=\frac{h\Delta T}{\displaystyle \frac{k\Delta T}{D}} \end{align}\)
プラントル(Pr)数
動粘度と熱拡散率の比をとった無次元量です。
\(\displaystyle \begin{align} Pr=\frac{C_p{\mu}}{k}\\\\=\frac{\displaystyle \frac{\mu}{\rho}}{\displaystyle \frac{k}{{\rho}C_p}}=\displaystyle \frac{{\nu}}{{\alpha}} \end{align}\)
\(\ C_p\):熱容量[J/kg・K],\(\ {\mu}\):粘度[Pa・s],\(\ {\rho}\):密度[kg/m^3]
\(\ {\nu}\):動粘度[m^2/s],\(\ {\alpha}\):熱拡散率[m^2/s]
終わりに
最後まで読んで頂き、ありがとうございました!
他にもあるのでそちらも良ければ読んでみてください👇





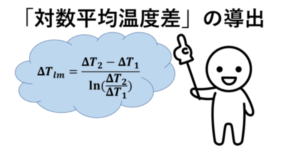


コメント