こんにちは、化工見習いです!
今回は算術平均温度差、対数平均温度差と向流並流の効率について少し書きたいと思います。
というのも、向流と並流の効率の違いについてずっと疑問だったのですが、昨日ふと思いついたので笑
まず各温度差をざっくり紹介し、2つの間にどのくらいのずれがあるのか、そしてなぜ向流の方が熱効率が良いのかについて数学的に考察します。
算術平均温度差と対数平均温度差とは
まず、対数平均温度差が登場する場面を抑えておきます。
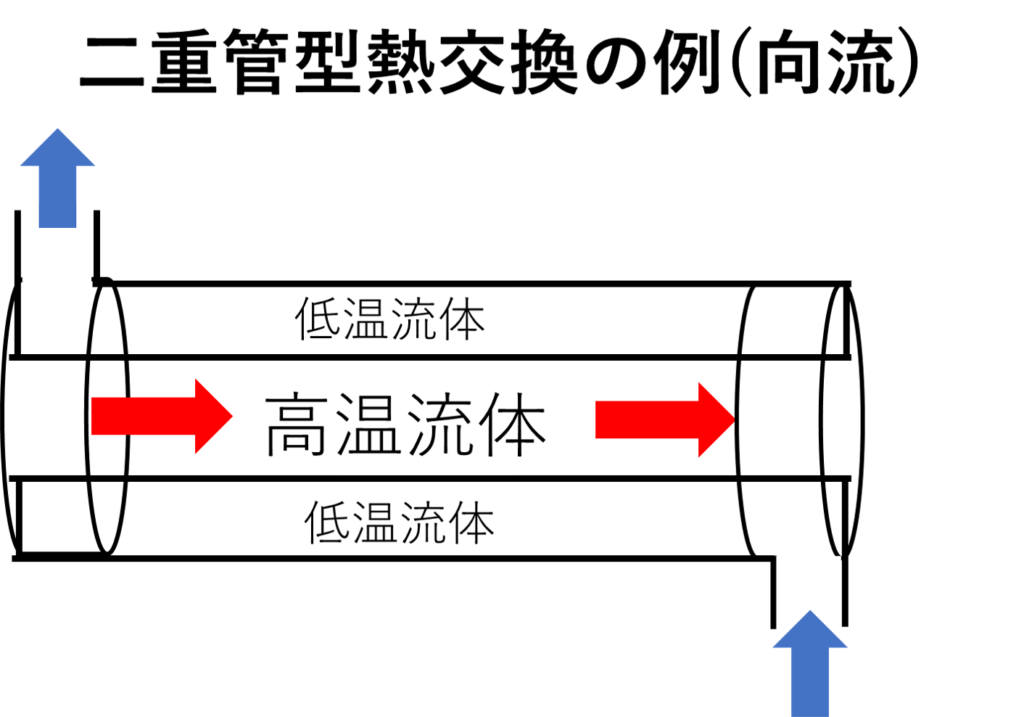
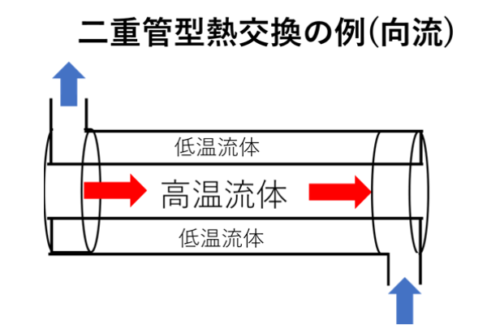
対数平均温度差は上の図の様に、温度差のある2つの流体を接触させて温度の調整を行う、熱交換において登場します。絵のセンスが乏しくてごめんなさい><
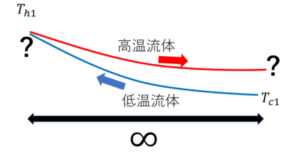
このような場合、各流体の、熱交換器長さ方向の温度分布は下の図のようになります。
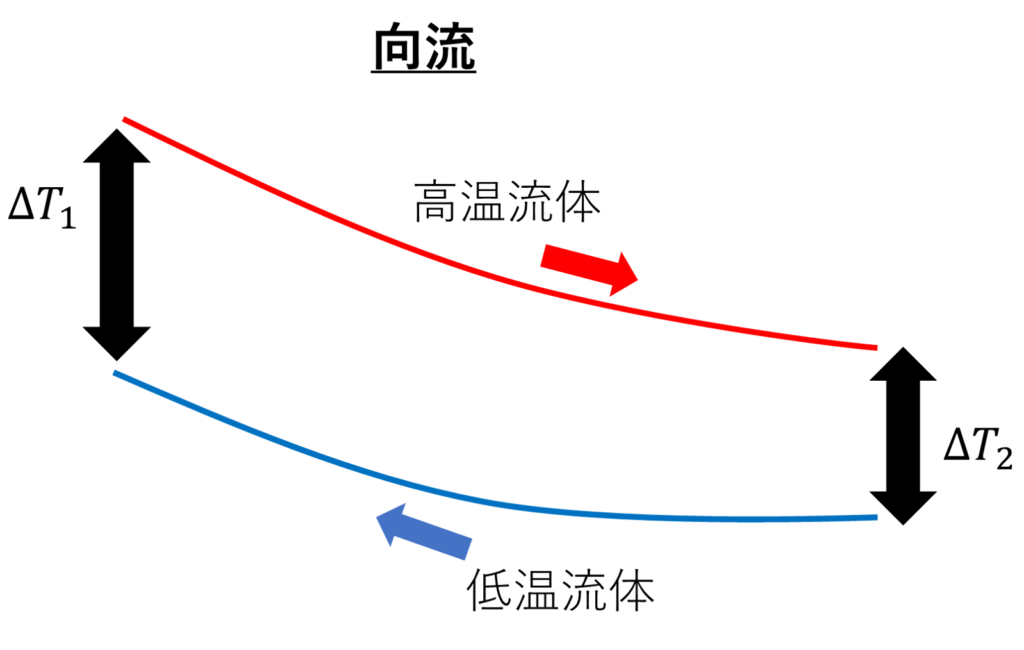
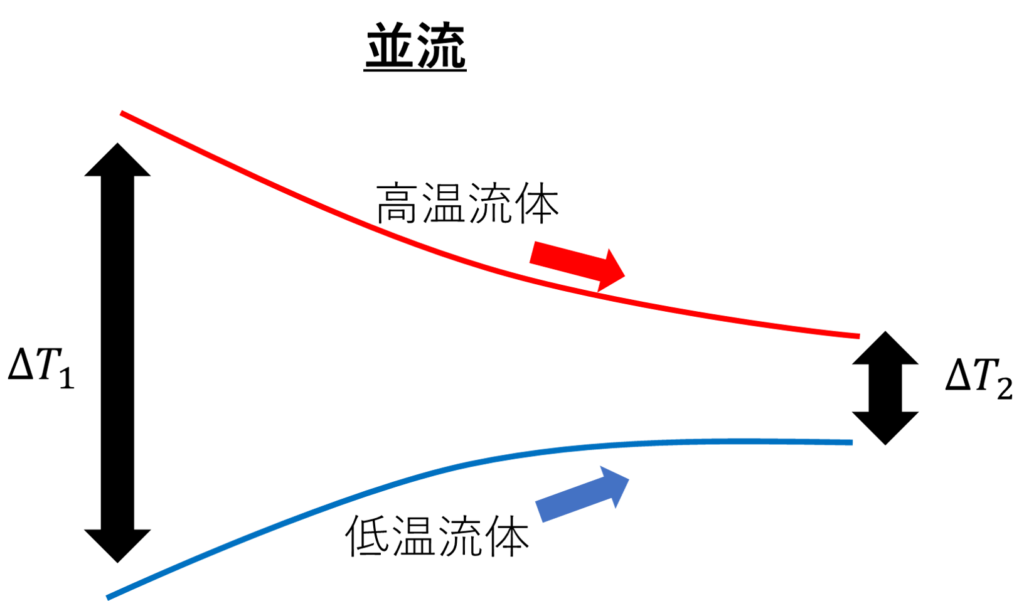
この時、高温流体と低温流体の温度差が長さ方向に一定ではありません。
これを、どの位置でも同じ温度差になるようにすると下の図のようになります。
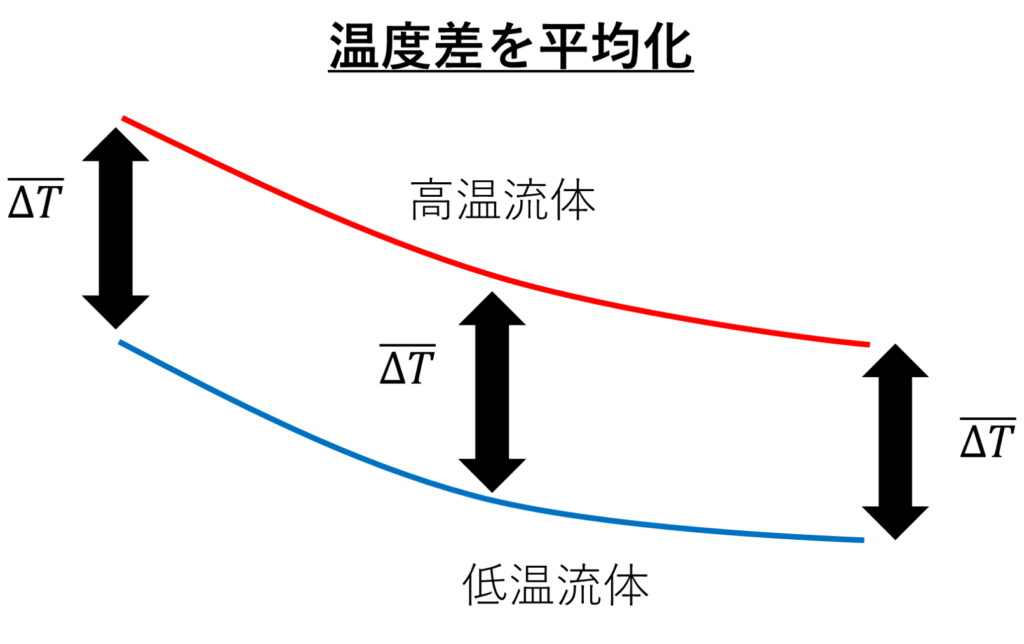
この平均化する手法こそが算術平均温度差や対数平均温度差なのです。
が、算術平均温度差は厳密には正しくなく、対数平均温度差を用いる必要があります。
紹介はこれくらいにして次に対数平均温度差と算術平均温度差のずれを考えます。
対数平均温度差と算術平均温度差のずれ
対数平均温度差と算術平均温度差のずれ-2 ずれ2 ずれ3改このグラフからもよく分かる通り、両側の温度差が大きければ大きい程、対数平均温度差と算術平均温度差のずれは大きくなることが分かります。
さらにこの結果を用いて、本題の「向流と並流の効率の違い」について考えてみます。
向流と並流の効率の違いを数学的に
向流と並流の効率改 向流2改このように、どんな熱交換長さにおいても向流の方が並流より熱交換率が高いことが分かりました!(多分)
補足の説明はこちら👇
補足1 補足2数学的に説明できても、感覚的に理解するのは難しい話です。ですが要するには、向流の方が並流よりも温度差が大きいわけです。よって熱交換量も向流の方が並流の場合よりも大きいのです。(どうにか感覚的に説明できないかと日々頭を悩ませている笑)
終わりに
なにか質問やご指摘などありましたら、コメントの方よろしくおねがいします><
今回は扱わなかった対数平均温度差の導出を記事にしましたので、興味のある方は是非こちらも見てください👇
化学工学技士(基礎)の解答と軽い解説を掲載していますのでよろしければご覧ください!
2021年度の解答と解説はこちら👇

2019年度の解答と解説はこちら👇
2018年度解答と解説はこちら👇